在学习编译原理之前，我们首先要知道为啥要学习？

大学课程为什么要开设编译原理呢？这门课程关注的是编译器方面的产生原理和技术问题，似乎和计算机的基础领域不沾边，可是编译原理却一直作为大学本科的必修课程，同时也成为了 研究生入学考试 的必考内容。我觉得有了解的必要性，文章由自己理解汇总，以达到考试及格为目的，若有错误，请留言指正，谢谢~

考试预估重点：文法、正规式、自动机、语法推导树。

一、什么是编译（理解）

1.1 计算机程序设计语言及编译

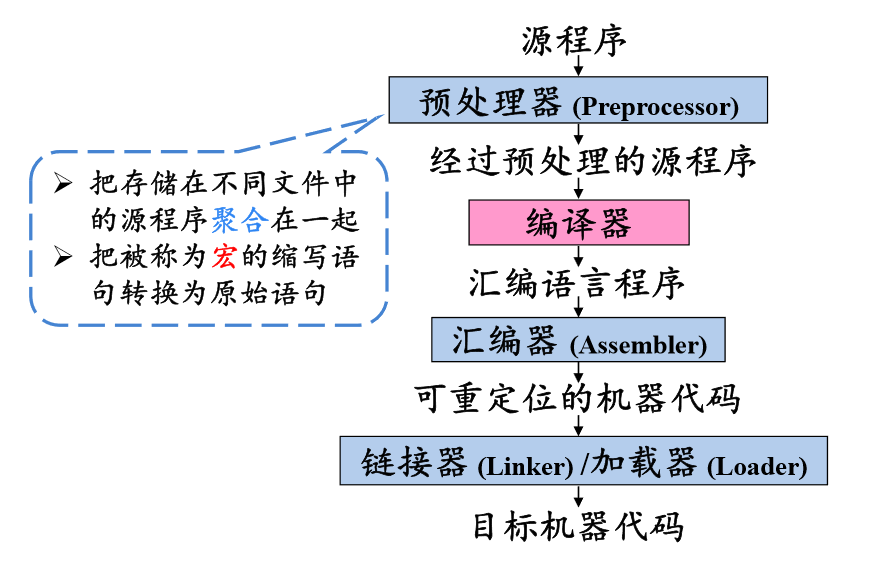
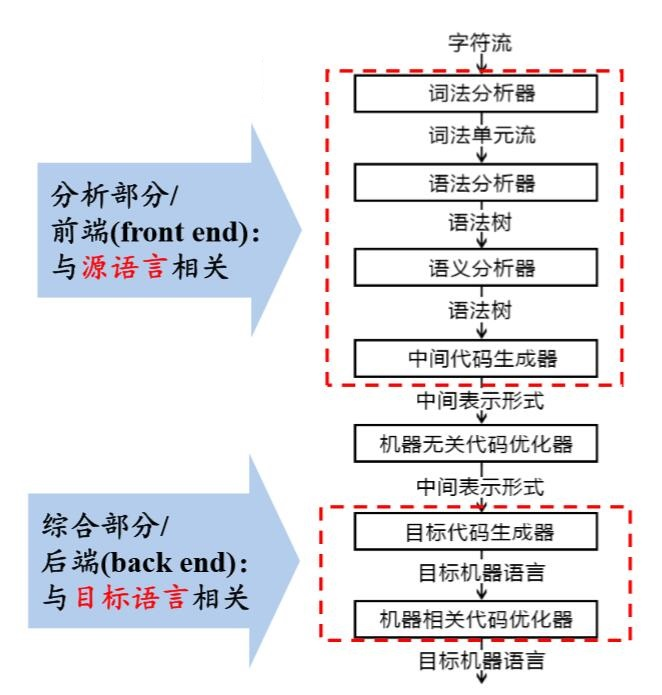
1.2 编译器在语言处理系统中的位置

1.3 编译系统的结构

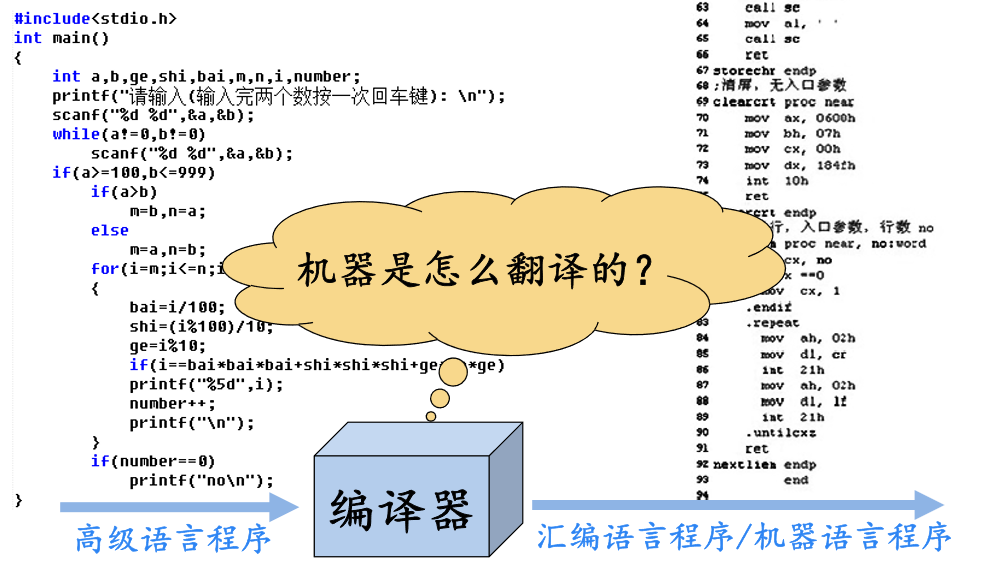
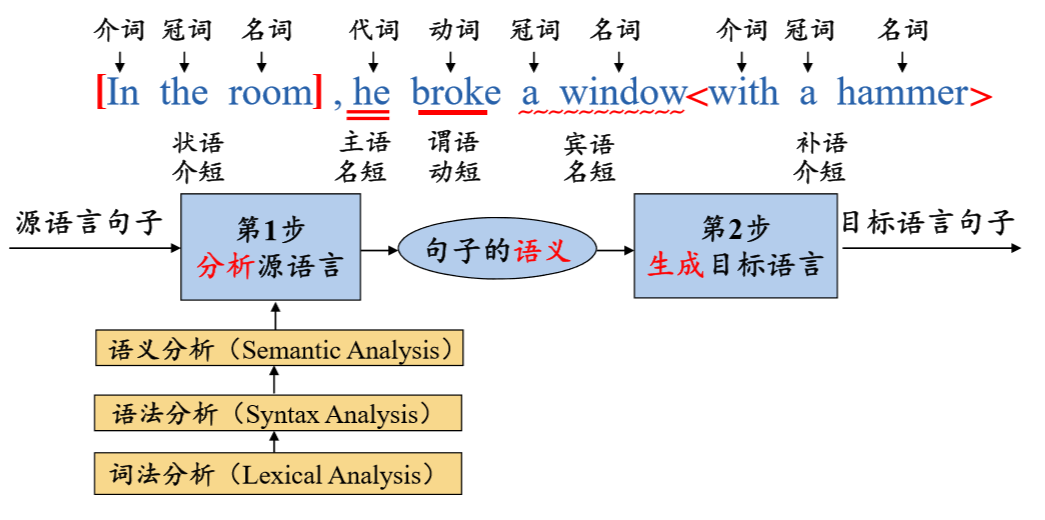
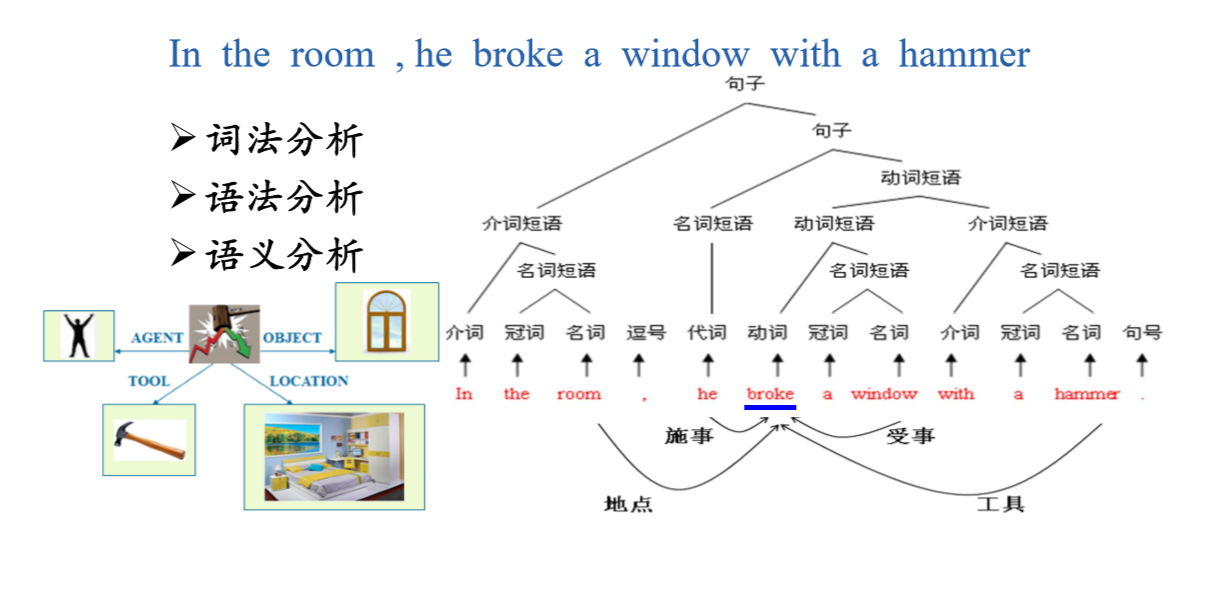
1.4 人工英汉翻译的例子

1.5 编译器的结构

二、文法（掌握）

认识终结符和非终结符
文法的类型
判断一个串是否为某个文法的句型

2.1 认识终结符和非终结符

终结符：不能单独出现在推导式的左边（一般用小写字母表示）

非终结符：可以拆分的元素，在推导式的右边（一般用大写字母表示）

例1：判断下面那些是终结符，那些是非终结符？

有文法G2[S]为：
S->Ap
S->Bq
A->a
A->cA
B->b
B->dB

答：S是开始符，S、A、B为非终结符、而p、q、a、b、c、d为终结符。

2.2 文法的类型

2.2.1 几种文法的理解

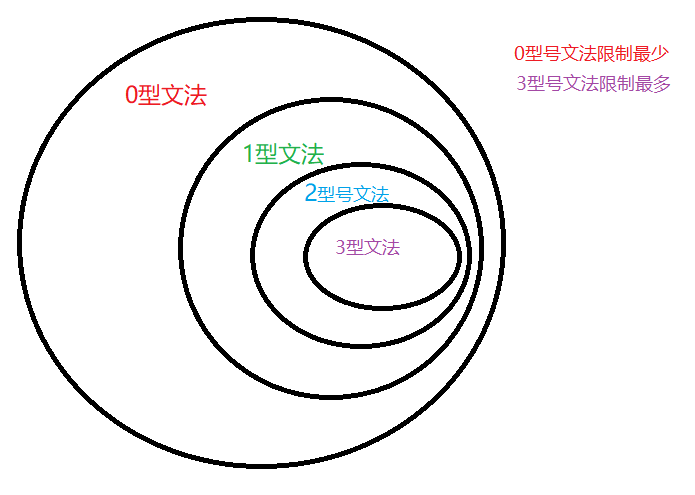
0型文法

设G=（Vn，Vt，P，S），Vn表示非终结符，Vt表示终结符，P表示整个集合，S表示开始符。如果每个产生式α->β是这样一种结构，α属于（Vn∪Tt）^* 且至少含有一个非终结符，而β属于（Vn∪Tt）^*，则G是一个0型文法，0型文法也成为短语文法。0型文法是这几个文法中限制最少的一个。

如： Aa->b,A->aBa 算是0型文法，而ab-A，a->A 则不算0型文法。

1型文法

1型文法又称上下有关文法，在0型文法的基础上每一个α->β，都有|β|>=|α|，这里的|β|表示 β的长度。

如：B->aB，|β|长度为2，|α|长度为1，则属于1型文法，而aB->B，则不属于1型文法。

2型文法

2型文法又称上下文无关文法，，它对应下推自动机，2型文法是在1型文法的基础上再满足，每一个α->β都有α是非终结符。

如：A->Ba，则属于2型文法，而Ab->Bab虽然符合1型文法，但是不符合2型文法。

3型文法

3型文法又称正规文法，它对应有限状态自动机，它是在2型文法的基础上再满足，A->a|aB（右线性）或者

A->a|Ba（左线性）。

如：A->a，A->aB，B->a，B->cB，则符号3型文法，但如果推导式为A->ab，A->aB，B->a，B->cB 或者 A->a，A->Ba，B->a，B->cB 则不符合3型文法。

例2：请判断文法G属于那一类文法？

A->ε|aB
B->Ab|a

答：

1、我们分开来写，应该是：A->ε A->aB B->Ab B->a
2、我们先来判断是否符合0型文法：0型文法规定左边必须有非终结符，那么这些都是符合的。
3、我们再来看是否符合1型文法：1型文法规定从小推到大，也符合。
4、我们再来看是否符合2型文法：2型文法规定左边必须是非终结符，也满足。
5、我们继续看是否符合3型文法：规定只能符合右线性或者左线性，那么前面一个应该是符合右线性的，后面一个是符合左线性的。所以综合起来就不符合3型文法了。

最终答案得出此文法属于2型文法。

2.2.2 几种文法的关系

三、正规式（掌握）

正规式又称正则表达式，一个正规式对应一个正规文法。

3.1 正规式与正规文法之间的转换

|       | 文法产生式 | 正规式 |
| ----- | ---------- | ------ |
| 规则1 | A->xB,B->y | A=xy   |
| 规则2 | A->xA|y   | A=x^*y |
| 规则3 | A->x,A->y  | A=x|y |

例3：

文法G[S]:S->xSx|y所描述的语言是_____（n>=0）
A.(xyx)^*
B.xyx^*
C.xy^*x
D.x^*yx^*

解题思路：将原生成式分开S->xS|y，S->Sx|y，S->xS|y正则式为x^*y，S->Sx|y正则式为yx^*，所以合起来为x^*yx^*，正确答案选D

例4：

语言L=｛a^mb^n|m>=0,n>=1｝的正则表达式是_____。
A.a^*bb^*
B.aa^*bb^*
C.aa^*b^*
D.a^*b^*

解题思路：可以直接代入值进行筛选答案，也可直接判断，因为n>=1，所以至少有一个b，a可以没有，所以正确答案选择A

四、有限自动机（掌握）

有限自动机又称为有穷自动机。

NFA与DFA的定义
NFA转化为DFA
正规表达式与有限自动机之间的转化

4.1 NFA与DFA的定义

4.1.1确定的有限自动机（DFA）的定义

一个有穷自动机M是一个五元组：

M=（S，∑，f，S0，Z）

S是一个有限状态集合
∑是一个字母表，它的每个元素称为一个输入字符
f是一个从S✖∑至S的单值部分映射，f（S，a）=s‘ 意味着：当现行状态为s，输入字符为a时，将状态到下一状态s‘。我们称为s‘为s的一个后继状态。
S0∈S，是唯一的初态。
Z⊆S，是一个终态集。

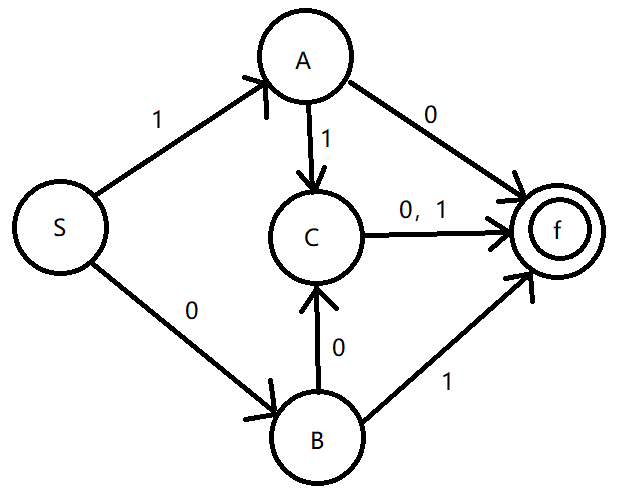
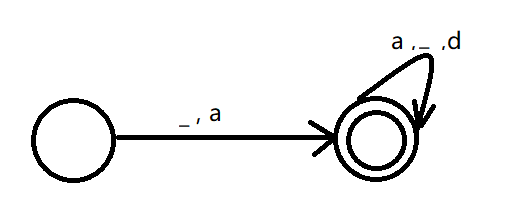
例5：画出下列DFA状态转换图：

DFA=({S,A,B,C,f},{1,0},F,S,{f}),为了不混淆，F在下方用K表示。
其中：K(S,0)=B,K(S,1)=A,K(A,0)=f,K(A,1)=C,K(B,0)=C,K(B,1)=f,k(C,1)=f;

解题思路：{S,A,B,C,f}是一个状态集合；{1,0}是输入字符；F是一个映射，S是初态，{f}是一个终态。K(S,0)=B表示为S状态输入0变到状态B，其他类似。

所以状态转换图为：

4.1.2 不确定的有限自动机（NFA）的定义

一个有穷自动机M是一个五元组：

M=（S，∑，f，S0，Z）

S是一个有限状态集合
∑是一个字母表，它的每个元素称为一个输入字符
f是一个从S✖∑至S的单值部分映射，f（S，a）=s‘ 意味着：当现行状态为s，输入字符为a时，将状态到下一状态s‘。我们称为s‘为s的一个后继状态。
S0⊆S，是一个非空初态集。
Z⊆S，是一个终态集。

4.2 NFA转化为DFA

例6：已知不确定的有限自动机（NFA）如图所示，采用子集法将其确定化为DFA的过程如下表示：

I	I0	I1
{S,1,2,3}	{1,3,4,5,Z}	{2,3}
{1,3,4,5,Z}	T1	T3
{2,3}	{4,5,Z}	{2,3}
T2	{6}	T3
T1	{1,3,4,5,6,Z}	{5,Z}
{6}	T3	{5,Z}
{5,Z}	{6}	T3

状态集T1中不包括编号为（1）的状态；状态集T2中的成员有（2）；状态集T3等于（3）。

（1）A.2   B.4   C.3   D.5
（2）A.1,3,4,5,Z   B.2,3   C.6   D.4,5,Z
（3）A.{Z}   B.{6}   C.{4,5,Z}   D.{}

解题思路：表格中对应的I0表示I通过输入0得到的值，I1为I通过输入1得到的值，观察NFA可以得出正确答案为：

A；D；D

最后根据状态集画出DFA即可

4.3 正规式与有限自动机之间的转换

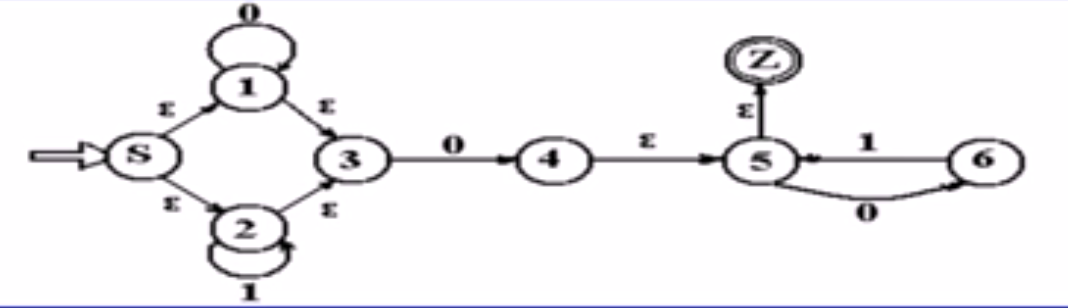
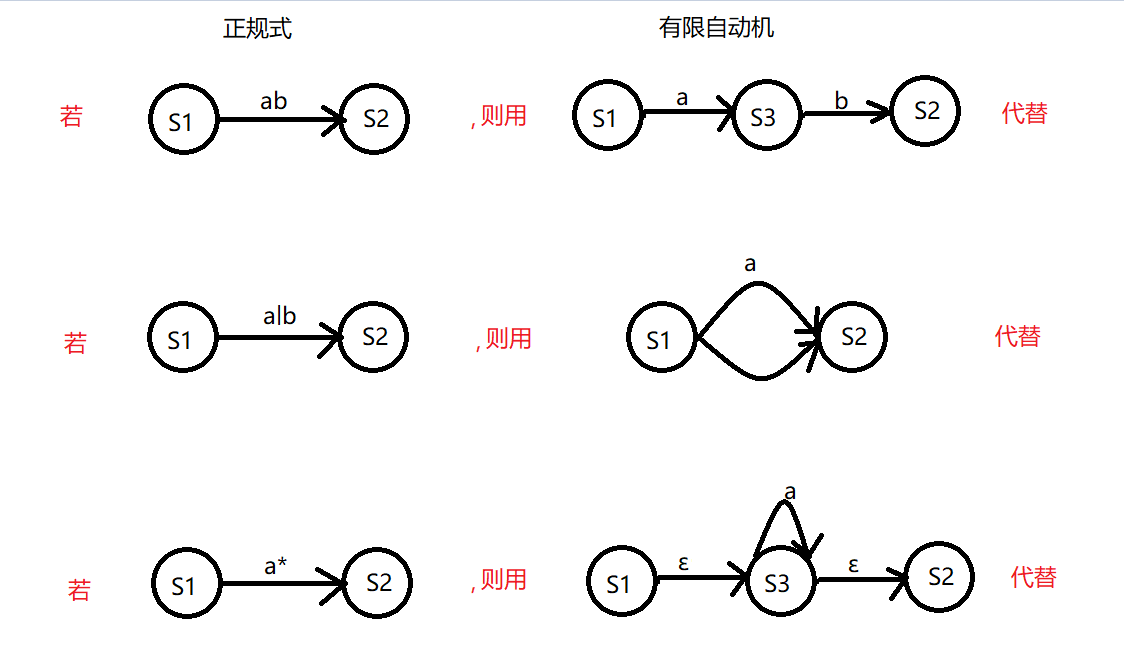
例7：把下面的正规式转换成有限自动机

(_|a)(_|a|d)^*

解题思路：下划线 a代表字母集 d代表数字集

可以画出下图有限自动机

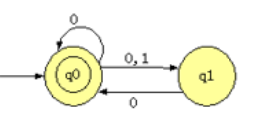
例8：某一非确定的有限自动机（NFA）的状态转换图如下图所示，该NFA等价的正规式是____。

A．0*|(0|1)0
B．(0|10)*
C．0*((0|1)0)*
D．0* (10)*

解题思路：q0既是初态也是终态（终态双圈）-->可以使空串（进入初态直接终态）现在ABCD都是闭包还不能排除选项。得到的串有可能全0、000000（0|1）0、0000000000000 10 0000000、101010101010.........，0是离散的，但每输入一个1后面就要一个0，根据排除法可以得出答案选择B

五、语法推导树（掌握）

5.1 语法树

一个语法树应具有以下特征：

每个结点都有一个标记，此标记是V的一个符号；
根的标记是S；
若一个结点n至少有一个它自己除外的子孙，并且有标记A，则A肯定在Vn中；
如果结点n的直接子孙，从左到右的次序是结点n1,n2...nk,其标记分别是：A1,A2...Ak，那么A->A1,A2...Ak，一定是P中的一个产生式。

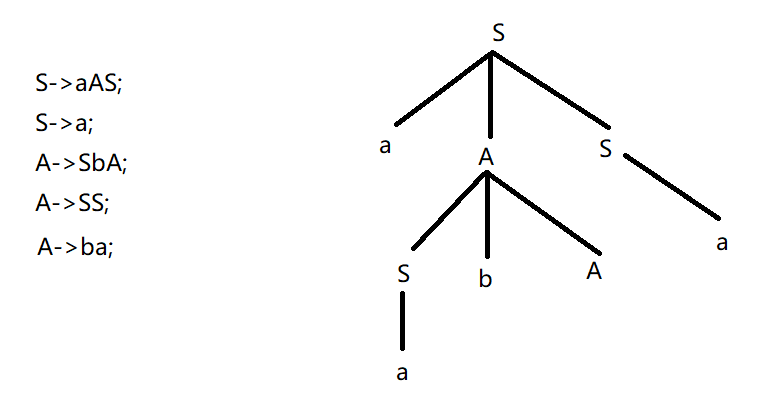
例9：

若文法G={{a,b},{S,A},S,P},其中：S->aAS|a; A->SbA|SS|ba;
请构造句型aabAa的推导树。

解题思路：首先拆开生成式，方便我们观察。最后通过推导画出推导树如下：

5.2 短语、简单短语、句柄

令G是一个文法，S是文法的开始符号，abc是文法G的一个句型。

如果有通过若干步S=>aAc，且A=>b，则称b是句型abc相对于非终结符A的短语。特别是，如有A=>b，则称b是句型abc相对于规则A->b的直接短语（也称简单短语）。一个句型的最左直接短语称为该项句型的句柄。

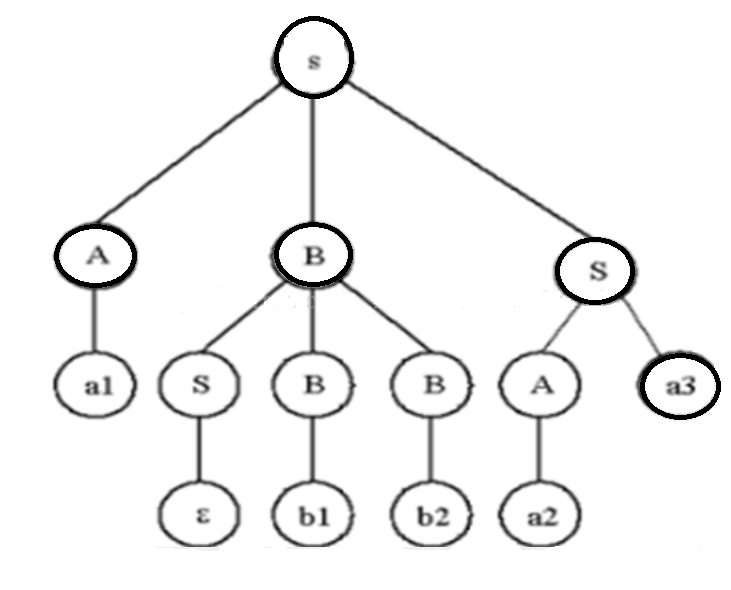
例10：一个上下文无关文法生成句子abbaa的推导树如下图所示，找出下面的这颗语法推导树的短语，直接短语，句柄。

简单理解短语、直接短语、句柄

短语：任意一颗子树中，如果根结点经过若干步才推导出了叶子结点，则这些叶子结点组成的序列就是相对于这棵子树的短语；

直接短语：属于短语，只不过不能经过若干步的推导了，必须一步就能推导出来叶子结点来，这些叶子结点组成的序列才是相对于这颗子树的直接短语；

句柄：属于直接短语，它是这些有直接短语的子树中最左边的那颗子树的直接短语。

答案:
短语：a1、ɛ、b1、b2、a2、a3
直接短语：因为这棵树的叶子结点是经过若干步推导出来的没有一步就推导出来的，所以没有直接短语。
句柄：从这些直接短语中找那个排在最左边的直接短语，即句柄，这道题的句柄就是a1

六、LL(1)文法（掌握）

判断是否是LL(1)文法
求生成式的FIRST、FOLLOW、SELECT集合

6.1 什么是LL(1)文法

第一个L代表从左向右扫描输入符号串，第二个L代表产生最左推导，1代表在分析过程中执行每一步推导都要向前查看一个输入符号——当前正在处理的输入符号。

对文法G的句子进行确定的自顶向下语法分析的充分必要条件是，G的任意两个具有相同左部的产生式A—>α|β 满足下列条件：

（1）如果α、β均不能推导出ε，则 FIRST(α) ∩ FIRST(β) = ∅。
（2）α 和 β 至多有一个能推导出 ε。
（3）如果 β *═> ε，则 FIRST(α) ∩ FOLLOW(A) = ∅。
将满足上述条件的文法称为LL(1)文法。

6.2 求FIRST集合

求解规则：计算各个文法符号X的FIRST(X)时，不断应用下列规则，直到再没有新的终结符号或者ε可以被加入到任何FIRST集合中为止。

1.如果X是一个终结符号，那么FIRST(X) = X。

2.如果X是一个非终结符号，且X -> Y1Y2 …Yk是一个产生式，其中k ≥ 1，那么如果对于某个i , a 在FIRST(Yi)中且ε在所有的FIRST(Y1)、FIRST(Y2)、….、FIRST(Yi-1)中，就把a加入到FIRST(X)中。也就是说，Y1…Yi-1 =>* ε。如果多于所有的j = 1,2,3,..,k , ε在FIRST(Yj)中，那么将 ε 加入到FIRST(X)中。比如，FIRST(Y1)中的所有符号一定在FIRST(X)中。如果Y1 不能推导出 ε ，那么，我们就不会再向FIRST(X)中加入任何符号，但是如果Y1 =>* ε ，那么我们就加上FIRST(Y2)，以此类推。

3.如果X -> ε 是一个产生式，那么将ε 加入到FIRST(X)中。

例11：求FIRST集合

E → TE'
E' → +TE' |ε
T → FT '
T' → *FT ' |ε
F → (E)|id

分析：

FIRST(E): 由E -> TE’可得FIRST(E) = FIRST(T)
FIRST(T): 由T -> FT’ 可得FIRST(T) = FIRST(F)
FIRST(F): 由F -> (E)和F -> id 可得FIRST(F) = { ( , id };
FIRST(T’): 由T’-> FT’ 和 T’-> ε 可得FIRST(T’) = { , ε };
FIRST(E’): 由E’-> +TE’ 和 E’-> ε可得FIRST(E’) = { + , ε };

答案：

FIRST ( E ) = { ( id }
FIRST ( E' ) = { + ε }
FIRST ( T ) = { ( id }
FIRST ( T' ) = { * ε }
FIRST ( F ) = { ( id }

6.3 求FOLLOW集合

求解规则：计算所有非终结符号A的FOLLOW(A)集合时，不断应用下列规则，直到再没有新的终结符号可以被加入到任意FOLLOW集合中为止。

1.将 $ 放到FOLLOW(S)中，其中S是开始符号，而 $ 是输入右端的结束标记。

2.如果存在一个产生式 A -> αBβ ， 那么FIRST(β)中除 ε之外的所有符号都在FOLLOW(B)中。

3.如果存在一个产生式A -> αB，或存在产生式 A -> αBβ 且 FIRST(β)包含 ε ，那么FOLLOW(A)中的所有符号都在FOLLOW(B)中。

例12：求FOLLOW集合

E → TE'
E' → +TE' |ε
T → FT '
T' → *FT ' |ε
F → (E)|id

分析：

FOLLOW(E): 由F -> (E)可得，FOLLOW(E) = { ) ，$}
FOLLOW(E’): 由E -> TE’ 和 E’-> +TE’ 可得，FOLLOW(E’) = FOLLOW(E)
FOLLOW(T): 由E -> TE’、E’-> +TE’ 和 E’-> ε 可得，FOLLOW(T) = FIRST(E’) / ε +FOLLOW(E) + FOLLOE(E’ )
FOLLOW(T’): 由T -> FT’ 和 T’-> *FT’ 可得，FOLLOW(T’) = FOLLOW(T)
FOLLOW(F): 由T -> FT’、T’-> *FT’ 和 T’-> ε 可得，FOLLOW(F) = FIRST(T’) / ε +FOLLOW(T) + FOLLOW(T’)

答案：

FOLLOW(E) = { ) ，$}
FOLLOW(E’) = FOLLOW(E) = { ) ，$}
FOLLOW(T) = FIRST(E’) / ε +FOLLOW(E) + FOLLOE(E’) = {+ , ) , $}
FOLLOW(T’) = FOLLOW(T) = {+ , ) , $}
FOLLOW(F) = FIRST(T’) / ε +FOLLOW(T) + FOLLOW(T’) = {* , + , ) , $}

6.4 求SELECT集合

求解规则：使用以下2个规则套用即可

1.如果ε∉FIRST（a），那么SELECT（A→a）=FIRST（a）

2.如果ε∈EFIRST（a），那么SELECT（A→a）=（FIRST（a）-{}）U FOLLOW（A）

例13：求SELECT集合

(1) E → T E '
(2) E '→ + T E '
(3) E '→ ε
(4) T → F T '
(5) T ' → * F T '
(6) T ' → ε
(7) F → ( E )
(8) F → id

分析：

X	FIRST( X )	FOLLOW( X )
E	( id	$ )
E '	+ ε	$ )
T	( id	+ ) $
T '	* ε	+ ) $
F	( id	* + ) $

答案：

SELECT (1)= { ( id }
SELECT (2)= { + }
SELECT (3)= { $ ) }
SELECT (4)= { ( id }
SELECT (5)= { * }
SELECT (6)= { + ) $ }
SELECT (7)= { ( }
SELECT (8)= { id }

<待更新...>

附件：

编译原理配套选择题下载

参考资料：

中国大学Mooc哈工大陈鄞编译原理视频：https://www.icourse163.org/course/HIT-1002123007

CSDN博文《原来编译原理可以这么学》

文章目录

商业转载请联系作者获得授权，非商业转载请注明本文出处及文章链接

编译原理从入门到放弃